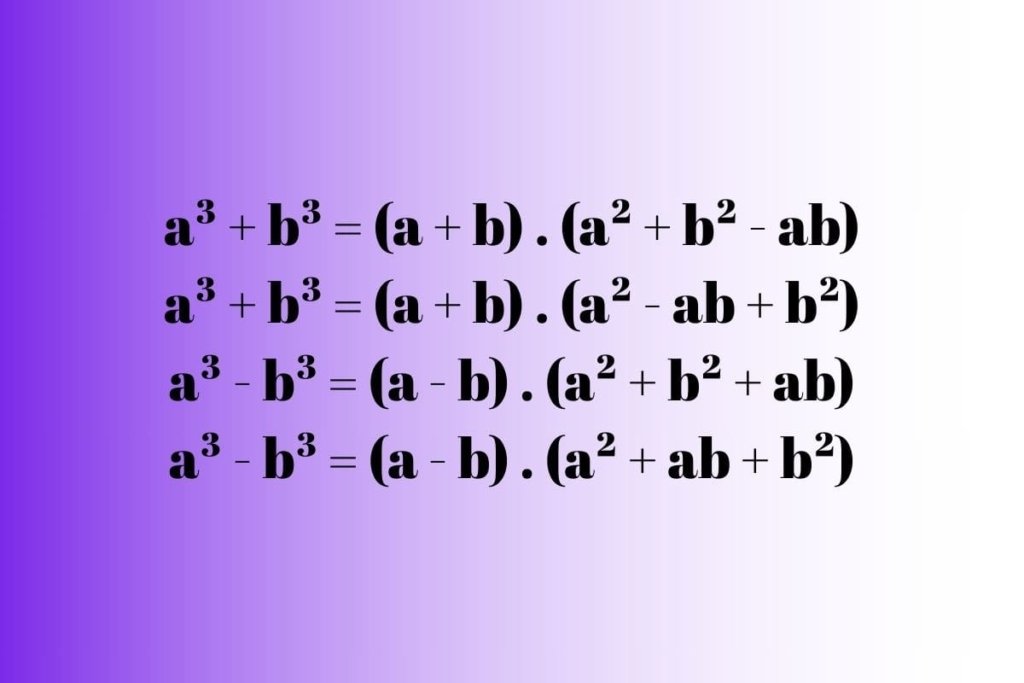Küp açılımı, ortaokuldan itibaren matematik derslerinde kullanılan önemli bir formüldür. Çarpanlara ayırma konusunun içerisinde yer almaktadır. Diğer çarpanlara ayırma formüllerine göre nispeten uzun olduğundan, öğrenciler açısından biraz zorlayıcıdır.
Çarpanlara ayırma başta olmak üzere birçok konudaki soruların çözümü için bu açılımın formülüne ihtiyaç duyulur. Yazının devamında, bu açılımın formülünü, püf noktaları ve örnek soruları bulabilirsiniz.
Buradaki açılma küp açılımları denilmesinin temel nedeni, sayıların üzerindeki kuvvetin 3 olmasıdır. Örneğin; (a + b)³ veya (x – y)³ şeklindeki açılımdaki kuvvet 3 olduğunda, küp olarak okunmaktadır. Eğer kuvvet 2 olsaydı, yani (c – m)² şeklinde ifadeler, kare olarak ifade edilmektedir.
Bu Yazıda Neler Var?
- Küp Açılımı Nedir?
- Küp Açılımı Formülleri
- 1 – İki Küpün Toplamı
- 2 – İki Küpün Farkı
- 3 – İki Sayının Toplamlarının Küpü
- 4 – İki Sayının Farklarının Küpü
- Küp Açılımı Formüllerinin Öğrenmenin Kolay Yolları
- Küp Açılım Dönüşümleri
- Küp Açılımı Örnekleri
- Küp Açılımı Örnek Sorular ve Cevaplar
- Küp Açılımı ile İlgili Sık Sorulan Sorular
- 1 – Küp Açılımı Formülleri Kaçıncı Sınıfta Kullanılmaya Başlar?
- 2 – Küp Açılımından İşaretler Nasıl Belirlenir?
- 3 – Kaç Tane Küp Açılımı Formülü Vardır?
Küp Açılımı Nedir?
Küp açılımı; iki sayının toplamının veya farkının küpünün nasıl alınacağını gösteren formüldür. Ancak söz konusu açılımın tek bir formülü yoktur. Zira sayıların toplamının veya farkının küpleri alınabildiği gibi iki küpün toplamı ve iki küpün farkının açılımları da gösterilebilmektedir.
Çarpanlara ayrıma konusu içerisinde çok sayıda formül ve kural vardır. Esasen bu konular, özdeşlikler konusu içerisinde yer almaktadır. Ancak çarpanlara ayırma ile birlikte verildiğinden, bu konu içerisinde değerlendirilmektedir.
Kuralların ve formüllerin kalıcı olması için şematize etme veya şekille gösterme yöntemleri kullanılır. Örneğin; iki sayının toplamının karesinin çizimi yapılarak anlatılmaktadır. Ancak küp açılımı çizimi yoktur. Dolayısıyla öğrencilerin direkt olarak formülleri önce ezberlemesi, sonrasında ise öğrenerek kalıcı hale getirmesi gerekir.
Küp Açılımı Formülleri
Birden fazla küp açılımı olduğundan, bunların her birinin ayrı formülü bulunmaktadır. Dolayısıyla küp açılımı formül ile gösterilirken, bunlardan uygun olan tercih edilir. Küp açılımlarının formülleri şu şekildedir:
1 – İki Küpün Toplamı
Bazı kaynaklarda tam küp açılımı olarak ifade edilen iki küpün toplamı, ayrı ayrı küpleri alınan sayıların toplanmasıdır. Bunun açılımı ise şu şekildedir:
- a³ + b³ = (a + b) . (a² + b² – ab)
2 – İki Küpün Farkı
İki küpün farkı, ayrı ayrı küpleri alınan sayıların çıkarılmasıdır. Bu farkın açılımı şu şekildedir:
- a³ – b³ = (a – b) . (a² + b² + ab)
3 – İki Sayının Toplamlarının Küpü
İki sayının toplamının küpü, parantez küp açılımı olarak da bilinmektedir. Bu açılıma ilişkin formül ise şu şekildedir:
- (a + b)³ = a³ + b³ + 3ab . (a + b)
- (a + b)³ = a³ + b³ + 3a²b + 3ab²
4 – İki Sayının Farklarının Küpü
İki sayının farklarının küpü veya x-y küp açılımı olarak bilinen formüldür. Bu formül ise şu şekildedir:
- (x – y)³ = x³ – y³ – 3xy . (x – y)
- (x – y)³ = x³ – y³ – 3x²y + 3xy²
Küp açılımı ile ilgili formüller bu şekildedir. Söz konusu formüllerden hangisinin kullanılacağı, tamamen soruya göre farklılık göstermektedir. Dolayısıyla şu tip sorularda bu formülü kullanmak gerekir veya şunları görünce bu formülü kullanın gibi ifadeler küp açılımı için geçerli değildir.
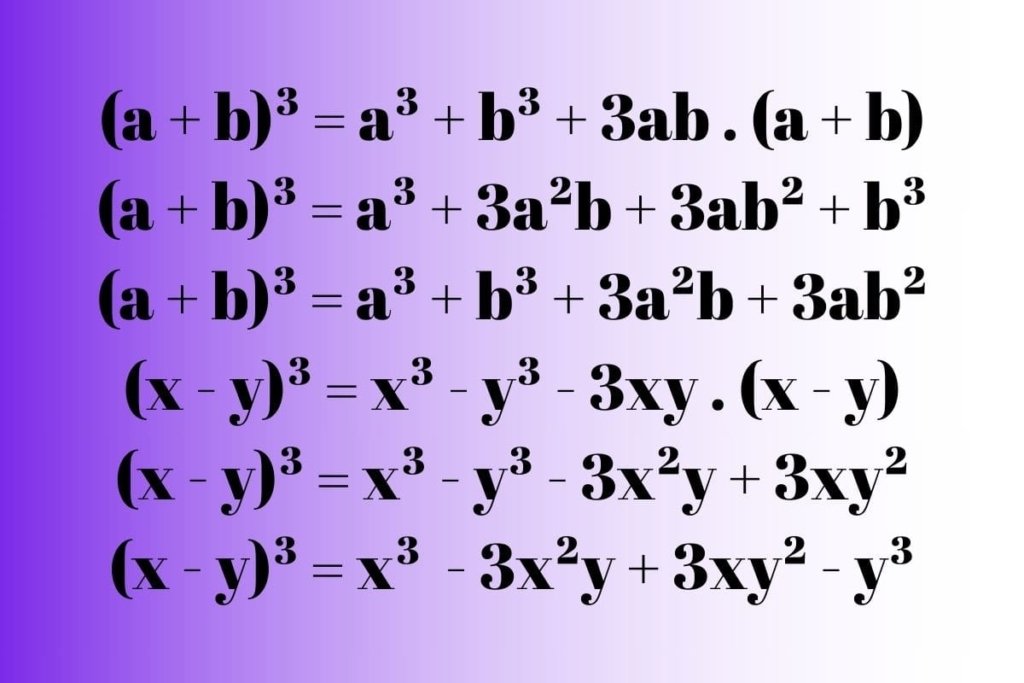
İki sayının toplamının küpü ve iki sayının farklarının küpü için ikişer tane formül bulunmaktadır. Buradaki iki açılım aslında birbirine tamamen eşittir ve birbirinin aynısıdır. Sorunun gidişatına göre bunlardan uygun olanın kullanılması, çözümü kolaylaştırır. Ancak ikisinden birinin tercih edilmesi ile de sorular çözülebilmektedir.
Küp Açılımı Formüllerinin Öğrenmenin Kolay Yolları
Küp açılımı, diğer özdeşlikler ve çarpanlara ayırma kurallarına göre nispeten daha uzundur. Ayrıca bilinmeyenlerin kuvvetleri ve terimlerin işaretleri arasında bir düzen bulunmamaktadır. Dolayısıyla bu formülleri öğrenmek zordur. Ancak bazı basit düzenlemeler ve püf noktalar ile bu açılımların öğrenilmesi çok daha kolay olmaktadır.
Her bir formül için basit düzenleme ve bazı püf noktalar vardır. İşte o düzenlemeler:
- a³ + b³ = (a + b) . (a² + b² – ab)
Küp toplamı açılımı olarak bilinen bu ifadenin öncelikle aşağıdaki gibi düzenlenmesi gerekir:
- a³ + b³ = (a + b) . (a² – ab + b²)
Bu düzenlemeden sonra a ve b ifadelerinin tüm işaretlerinin pozitif, ab ifadesinin işaretinin ise negatif olduğu fark edilmelidir. Ayrıca a³ + b³ ifadesinin açılımı, (a + b) ile başlamaktadır. Yani açılım, kendisi ile başlar. Ayrıca a² başta ve b² ise sondadır.
- a³ – b³ = (a – b) . (a² + b² + ab)
Küp farkı olarak bilinen bu ifade için de benzer şekilde bir düzenleme yapılması gerekir.
- a³ – b³ = (a – b) . (a² + ab + b²)
Burada da açılım kendisiyle, yani (a – b) ile başlamaktadır. Yine benzer olarak a² başta ve b² ise sonda yer almaktadır.
- (a + b)³ = a³ + b³ + 3a²b + 3ab²
Bu ifadenin ise öncelikle aşağıdaki gibi düzenlenmesi gerekir:
- (a + b)³ = a³ + 3a²b + 3ab² + b³
Buradaki tüm terimlerin işaretinin pozitif olduğu, 3ab’li ifadelerde önce a’nın kuvvetinin 2, daha sonraki terimde ise b’nin kuvvetinin 2 olduğu fark edilmelidir.
- (x – y)³ = x³ – y³ – 3x²y + 3xy²
Farkın küpü olan bu ifadede düzenleme şöyle yapılır:
- (x – y)³ = x³ – 3x²y + 3xy² – y³
Burada önemli olan işaretlerdir. İşaretleri yerleştirirken y’nin kuvvetinin 1 ve 3 olduğu terimlerde negatif (-) işaret kullanılır.
Küp Açılım Dönüşümleri
Küp açılımı formüllerinin kısa sürede öğrenilmesi ve etkili şekilde sorularda kullanılması için farklı tipteki açılımların bilinmesi gerekir. Farklı açılımlar şu şekildedir:
| Formül | Açılım |
| a³ + b³ | (a + b) . (a² + b² – ab) |
| (a + b) . (a² – ab + b²) | |
| a³ – b³ | (a – b) . (a² + b² + ab) |
| (a – b) . (a² + ab + b²) | |
| (a + b)³ | a³ + b³ + 3ab . (a + b) |
| a³ + 3a²b + 3ab² + b³ | |
| a³ + b³ + 3a²b + 3ab² | |
| (x – y)³ | x³ – y³ – 3xy . (x – y) |
| x³ – y³ – 3x²y + 3xy² | |
| x³ – 3x²y + 3xy² – y³ |

Küp Açılımı Örnekleri
Buradaki formüllerin kalıcı olması için örnekler üzerinde nasıl uygulandığının görülmesi yararlı olacaktır. Bazı küp açılımı örnekleri şu şekildedir:
- (x – 1)³ = x³ – 3x² + 3x – 1
- (a + 2)³ = a³ + 6a² + 12a + 8
- a³ + 1 = (a + 1) . (a² – a + 1)
Buradaki örnekte a’nın küpü ile 1 toplanmıştır. 1, aynı zamanda kendisinin küpüdür. Dolayısıyla işlem yaparken a³ + 1³ açılımından yararlanılır.
- a³ – 8 = (a – 2) . (a² + 2a + 4)
Buradaki örnekte ise 8’in aslında 2’nin küpü olduğu fark edilmelidir. Bu durum çarpım tablosu üzerinde de görülmektedir. Sonrasında ise a³ – 2³ açılımı yapılır.
Küp Açılımı Örnek Sorular ve Cevaplar
Örnek sorular ve bunların cevapları, açılımların daha iyi öğrenilmesine ve nasıl uygulandıklarının görülmesine yardım etmektedir. Bundan dolayı öğrencilerin konu tekrarlarından sonra bol bol örnek soru çözmesi gerekmektedir.
1 – İki reel sayının çarpımları 11, toplamları ise 4’dir. Bu reel sayıların küplerinin toplamı kaçtır?
Soru incelendiğinde ilk olarak neyin sorulduğuna bakılmalıdır. Ayrıca neyin istendiği de tespit edilmelidir. Bu bağlamda verilenler ve istenenler şu şekildedir:
a + b = 4 ve a.b = 11
a³ + b³ = ?
Açılımların tamamı incelenerek, içerisinde a + b, a.b ve a³ + b³ olan formül bulunmalıdır. Tabloya bakıldığında bu formül net olarak görülmektedir:
- (a + b)³ = a³ + b³ + 3ab . (a + b) açılımında verilenleri yerine koymak gerekir. Bunun için (a + b) yerine 4 ve a.b yerine ise 11 yazılmalıdır.
- (4)³ = a³ + b³ + 3.11.(4)
- 64 = a³ + b³ + 132
- 64 – 132 = a³ + b³
- a³ + b³ = -68
2 – Buradaki (a³ + 64) ifadesini çarpanlarına ayırınız.
Bu ifadenin çarpanlarına ayrılması için kullanılacak olan formülün tespit edilmesi gerekir. İlk bakışta ilk sayının küpü varken, ikinci sayının ise küpünün olmadığı görülür. Ancak 64 = 4³ şeklindedir. Yani 64 de küp sayıdır. Dolayısıyla aslında soru şu şekildedir: a³ + 4³
- a³ + b³ = (a + b) . (a² – ab + b²) açılımında b görülen yerlere 4 yazılarak soru çözülür.
- a³ + 4³ = (a + 4) . (a² – a4 + 4²) ifadesinin düzenlenmesi gerekmektedir.
- a³ + 64 = (a + 4) . (a² – 4a + 16)

Küp Açılımı ile İlgili Sık Sorulan Sorular
Küp açılımı ile ilgili sık sorulan sorular ve bunların yanıtları şu şekildedir:
1 – Küp Açılımı Formülleri Kaçıncı Sınıfta Kullanılmaya Başlar?
Küp açılımına dair formüller ilk defa 8.sınıfta kullanılmaktadır.
2 – Küp Açılımından İşaretler Nasıl Belirlenir?
Açılımlarda işaretler belirlenirken, pozitif terimin tek başına olduğu tüm terimler pozitifken, negatif terimin kuvveti çift olduğunda pozitif, tek olduğunda ise negatiftir.
3 – Kaç Tane Küp Açılımı Formülü Vardır?
Dört farklı küp açılımı bulunur. Bu açılımları farklı şekillerde yazmak mümkündür.